Aller au contenu

Les opérateurs booléens⚓︎

image

1. Repères historiques⚓︎

En 1847, le britannique George BOOLE inventa un formalisme permettant d'écrire des raisonnements logiques : l'algèbre de Boole. La notion même d'informatique n'existait pas à l'époque, même si les calculs étaient déjà automatisés (penser à la Pascaline de 1642).

Bien plus tard, en 1938, les travaux de l'américain Claude SHANNON prouva que des circuits électriques peuvent résoudre tous les problèmes que l'algèbre de Boole peut elle-même résoudre. Pendant la deuxième guerre mondiale, les travaux d'Alan TURING puis de John VON NEUMANN poseront définitivement les bases de l'informatique moderne.

2. Algèbre de Boole⚓︎

L'algèbre de Boole définit des opérations dans un ensemble qui ne contient que deux éléments notés 0 et 1, ou bien FAUX et VRAI ,ou encore False et True (en Python)

Les opérations fondamentales sont :

  • la conjonction ("ET")
  • la disjonction ("OU")
  • la négation ("NON").

Dans toute la suite, x et y désigneront des Booléens (éléments d'une algèbre de Boole) quelconques, F désignera FAUX et V désignera VRAI.

2.1 Conjonction (AND)⚓︎

  • symbole usuel : & (appelé esperluette en français et ampersand en anglais)
  • français : ET
  • anglais (et Python) : and
  • notation logique : \(\wedge\)
  • notation mathématique : .

C'est l'opération définie par:

  • x & F = F
  • x & V = x

Puisque l'algèbre de Boole ne contient que deux éléments, on peut étudier tous les cas possibles et les regrouper dans un tableau appelé table de vérité:

Table de vérité de AND ❤

x y x & y
0 0 0
0 1 0
1 0 0
1 1 1

On représente souvent les opérateurs booléens à l'aide de portes logiques:

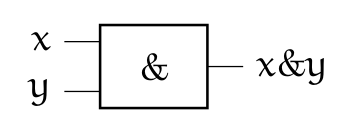
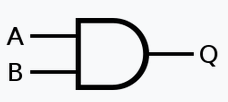
Notation usuelle en électronique : \(Q=A \wedge B\)

Exemples en Python⚓︎

🐍 Script Python
>>> n = 20
>>> (n % 10 == 0) and (n % 7 == 0)
False
>>> (n % 4 == 0) and (n % 5 == 0)
True

L'évaluation paresseuse⚓︎

Pouvez-vous prévoir le résultat du code ci-dessous ?

🐍 Script Python
>>> (n % 4 == 0) and (n % 0 == 0)
    ---------------------------------------------------------------------------

    ZeroDivisionError                         Traceback (most recent call last)

    <ipython-input-3-d8a98dcba9be> in <module>
    ----> 1 (n % 4 == 0) and (n % 0 == 0)


    ZeroDivisionError: integer division or modulo by zero

Évidemment, la division par 0 provoque une erreur.
Mais observez maintenant ce code :

🐍 Script Python
>>> (n % 7 == 0) and (n % 0 == 0)
False

On appelle évaluation paresseuse le fait que l'interpréteur Python s'arrête dès que sa décision est prise : comme le premier booléen vaut False et que la conjonction and est appelée, il n'est pas nécessaire d'évaluer le deuxième booléen.

2.2 Disjonction (OR)⚓︎

  • symbole usuel : | appelé pipe en anglais
  • français : OU
  • anglais (et Python) : or
  • notation logique : \(\vee\)
  • notation mathématique : \(+\)

C'est l'opération définie par:

  • x | V = V
  • x | F = x

On en déduit la table suivante:

Table de vérité de OR ❤

x y x or y
0 0 0
0 1 1
1 0 1
1 1 1

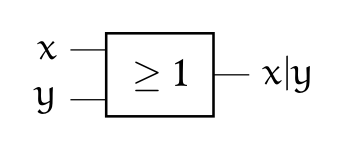
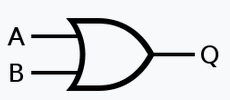
Notation usuelle en électronique : \(Q=A \vee B\)

Exemples en Python⚓︎

🐍 Script Python
>>> n = 20
>>> (n % 10 == 0) or (n % 7 == 0)
True
>>> (n % 4 == 0) or (n % 5 == 0)
True
>>> (n % 7 == 0) or (n % 3 == 0)
False

L'évaluation paresseuse (retour)⚓︎

Pouvez-vous prévoir le résultat du code ci-dessous ?

🐍 Script Python
>>> (n % 5 == 0) or (n % 0 == 0)

2.3 Négation (NOT)⚓︎

  • symbole usuel : ~
  • français : NON
  • anglais (et Python) : not
  • notation logique : \(\neg\)
  • notation mathématique : \(\overline{x}\)

C'est l'opération définie par:

  • ~V = F
  • ~F = V

On en déduit la table suivante:

Table de vérité de NOT ❤

x ~x
0 1
1 0

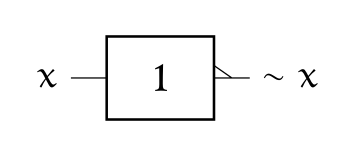
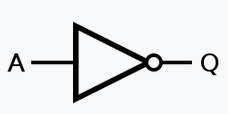
Notation usuelle en électronique : \(Q=\neg A\)

Exemples en Python⚓︎

🐍 Script Python
>>> n = 20
>>> not(n % 10 == 0)
False

2.4 Exercices⚓︎

Exercice 1

Comprendre ce mème : image

Exercice 2

Il existe une propriété appelé la distributivité en logique formelle.

Distributivité

a et (b ou c) = (a et b) ou (a et c)
a ou (b et c) = (a ou b) et (a ou c)

Démontrer les deux égalités de la distributivité à l’aide des tables de vérité suivantes distributivité

Exercice 3

Le mathématicien britannique Auguste de Morgan (1806–1871) a également contribué à développer l’algèbre de Boole à l’aide de son théorème :

Loi de Morgan

non (a ou b) = (non a) et (non b)
non (a et b) = (non a) ou (non b)

Démontrer ce théorème à l’aide des tables ci-dessous : loi de morgan

Exercice 4

Ouvrir le simulateur de circuits et créer pour chaque opération AND, OR, NOT un circuit électrique illustrant ses propriétés.

Exemple (inintéressant) de circuit :

ET OU

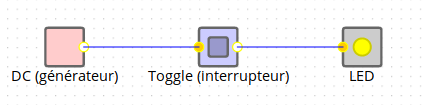
3. Fonctions composées⚓︎

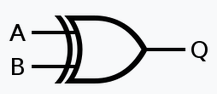
3.1 Disjonction exclusive XOR⚓︎

(en français OU EXCLUSIF)

En français, quand on dit “fromage ou dessert”, c’est l’un ou l’autre. Ce qui n’est pas le cas du OU utilisé dans les booléens. On appelle ou exclusif ou xor l’opération définie par

x ^ y = (x & ~y) | (~x & y)

Table de vérité de XOR ❤

x y x ^ y
0 0 0
0 1 1
1 0 1
1 1 0

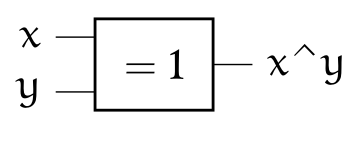
Le XOR joue un rôle fondamental en cryptographie car il possède une propriété très intéressante : \((x\wedge y)\wedge y=x\)

Si \(x\) est un message et \(y\) une clé de chiffrage, alors \(x\wedge y\) est le message chiffré. Mais en refaisant un XOR du message chiffré avec la clé \(y\), on retrouve donc le message \(x\) initial.

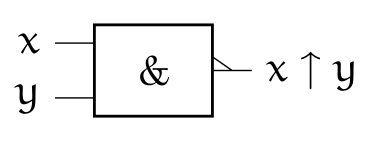
3.2 Fonction Non Et (NAND)⚓︎

x ↑ y = ~(x & y)

Table de vérité de NAND ❤

x y x ↑ y
0 0 1
0 1 1
1 0 1
1 1 0

3.3 Fonction Non Ou (NOR)⚓︎

x ↓ y = ~(x & y)

Table de vérité de NOR ❤

x y x ↓ y
0 0 1
0 1 0
1 0 0
1 1 0

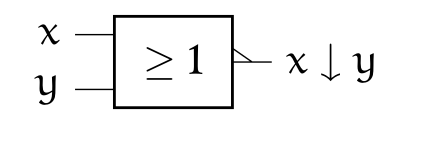
Il est temps de se reposer un peu et d'admirer cette vidéo :

Remarque :⚓︎

Les fonctions NAND ET NOR sont dites universelles : chacune d'entre elles peut générer l'intégralité des autres portes logiques. Il est donc possible de coder toutes les opérations uniquement avec des NAND (ou uniquement avec des NOR). Voir Wikipedia

Exercice 5

Calculer les opérations suivantes.

🐍 Script Python
1011011
&  1010101
----------


1011011
|  1010101
----------


1011011
^  1010101
----------
🐍 Script Python
1011011
&1010101
----------
1010001

1011011
|1010101
----------
1011111

1011011
^1010101
----------
0001110

3.4 Calculs en Python⚓︎

les opérateurs &, | et ^ sont utilisables directement en Python

🐍 Script Python
# calcul A
>>> 12 & 7
4
🐍 Script Python
# calcul B
>>> 12 | 7
15
🐍 Script Python
# calcul C
>>> 12 ^ 5
9

Pour comprendre ces résultats, il faut travailler en binaire. Voici les mêmes calculs :

🐍 Script Python
# calcul A
>>> bin(0b1100 & 0b111)
    '0b100'
🐍 Script Python
# calcul B
>>> bin(0b1100 | 0b111)
   '0b1111'
🐍 Script Python
# calcul C
>>> bin(0b1100 ^ 0b111)
    '0b1011'

Exercice 6 : préparation du pydéfi

Objectif : chiffrer (= crypter) le mot "BONJOUR" avec la clé (de même taille) "MAURIAC".

Protocole de chiffrage : XOR entre le code ASCII des lettres de même position.

🐍 Script Python
msg = "BONJOUR"
cle = "MAURIAC"

def crypte_lettre(lm, lc):
    a = ord(lm)
    b = ord(lc)
    c = a^b
    lettre = chr(c)

    return lettre

def crypte_mot(mot1, mot2):
    mot3 = ""
    for i in range(len(mot1)):
        car = crypte_lettre(mot1[i],mot2[i])
        mot3 = mot3 + car
    return mot3

crypte_mot(msg, cle)
'\x0f\x0e\x1b\x18\x06\x14\x11'

Exercice 7 (facultatif)

💡 Résolvez le pydéfi la clé endommagée

solution : lien

Complément : propriétés des opérateurs logiques⚓︎

Les propriétés suivantes sont facilement démontrables à l'aide de tables de vérités: (source : G.Connan)

Toutes ces lois sont aisément compréhensibles si on les transpose en mathématiques :

  • & équivaut à \(\times\)
  • \(|\) équivaut à \(+\)
  • \(\neg\) équivaut à \(-\)