Méthode du K-Nearest-Neighbours (KNN), ou les k-plus-proches-voisins⚓︎

Source

Comprendre le Machine Learning: L'algorithme du KNN
gilles lassus, Lycée François Mauriac / Bordeaux
Livre Prépabac 1ere, NSI spécialité

Pré-requis⚓︎

Savoir utiliser le module Pandas

Introduction⚓︎

L’algorithme des k plus proches voisins appartient à la famille des algorithmes d’apprentissage automatique (machine learning).

La méthode KNN est une méthode simple et efficace de classification. La classification est un enjeu majeur de l'Intelligence Artificielle :

la caméra d'une voiture autonome perçoit un panneau, mais quel est ce panneau ?
un grain de beauté est pris en photo par un dermatologue, ce grain de beauté est-il cancéreux ?
...

L’idée d’apprentissage automatique ne date pas d’hier, puisque le terme de machine learning a été utilisé pour la première fois par l’informaticien américain Arthur Samuel en 1959. Les algorithmes d’apprentissage automatique ont connu un fort regain d’intérêt au début des années 2000 notamment grâce à la quantité de données disponibles sur internet.L’algorithme des k plus proches voisins est un algorithme d’apprentissage supervisé, il est nécessaire d’avoir des données labellisées (c'est à dire disposant d'une étiquette descriptive ou label).

À partir d’un ensemble E de données labellisées, il sera possible de classer (déterminer le label) une nouvelle donnée (donnée n’appartenant pas à E). L’algorithme des k plus proches voisins est une bonne introduction aux principes des algorithmes d’apprentissage automatique ou machine learning, il est en effet relativement simple à appréhender.

Principes de fonctionnement⚓︎

Pour ceux qui aiment les vidéos, en voici une sur le fonctionnement de l'algorithme : L'algorithme du KNN

le principe du knn⚓︎

Si l'on prend le schéma ci dessous :

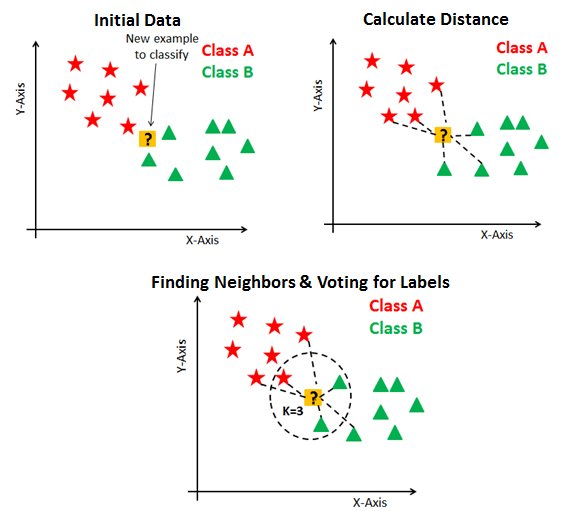
On va s'intéresser à un ensemble de données labellisées possédant 2 caractéristiques principales. On pourra modéliser cette ensemble à l'aide d'un graphique (d'ou l'utilisation de la librairie Pandas en travail préparatoire), où l'une des caractéristiques sera positionnée en abscisse et la seconde en ordonnée. Dans le modèle ci dessus, on a 2 labels "étoile rouge" et "triangle vert", avec 2 caractéristiques X en abscisse et Y en ordonnée.

Le but de notre algorithme est de détermine de quel label est notre point d'interrogation.

L'algorithme des plus proches voisins se base sur la distance entre un nouvel élément inconnu et ceux issus de l'ensemble d'apprentissage. Pour calculer cette distance, on va utiliser la distance euclidienne (on peut utiliser d'autres calculs de distance mais c'est la plus naturelle pour vous en première).

Distance euclidienne : si le point 1 a pour coordonnées (x1, y1) et le point 2 a pour coordonnées (x2,y2) :

distance(point1, point2) = \(\sqrt{(x_{1}-x_{2})^2+(y_{1}-y_{2})^2}\)

Formulation de l'algorithme : Pour prédire si notre point d'interrogation est une "étoile rouge" ou un "triangle vert", on peut formuler l'algorithme de prédiction comme suit :

📋 Texte

  1. Trouver, dans l'échantillon, les _k_ plus proches voisins de notre point d'interrogation.
  2. Parmi ces proches_voisins, trouver la classification majoritaire
  3. Renvoyer la classification majoritaire.

La notion de distance va être utilisée pour classifier les données.

Exercice 1⚓︎

Récupérer l’image ci-dessous et à l’aide d’un outil de traitement d’image (paint par exemple) placer les points A(5,0) et B(1,4) puis enfin le point I(3,3).

graphe1

De A ou de B, quel est le plus proche voisin de I ? Confirmer votre intuition par le calcul de la distance euclidienne entre I et A, puis entre I et B.

Question 1

questionRéponse

Quelle est la distance euclidienne entre I et A ?

3,6

Question 2

questionRéponse

Quelle est la distance euclidienne entre I et B ?

2,2

Question 3

questionRéponse

quel est le point le plus proche de I ?

B

Mise en Application⚓︎

Notre objectif : Nous allons reprendre le jeu de données sur les joueurs du top14 utilisé dans le travail préparatoire sur Pandas.

Question : si on croise une personne nous disant qu'elle veut jouer en top14, et qu'elle nous donne son poids et sa taille, peut-on lui prédire à quel poste elle devrait jouer ?

Dans toute idée de classification il y a l'idée de distance. Il faut comprendre la distance comme une mesure de la différence.

Comment mesurer la différence physique entre deux joueurs de rugby ?

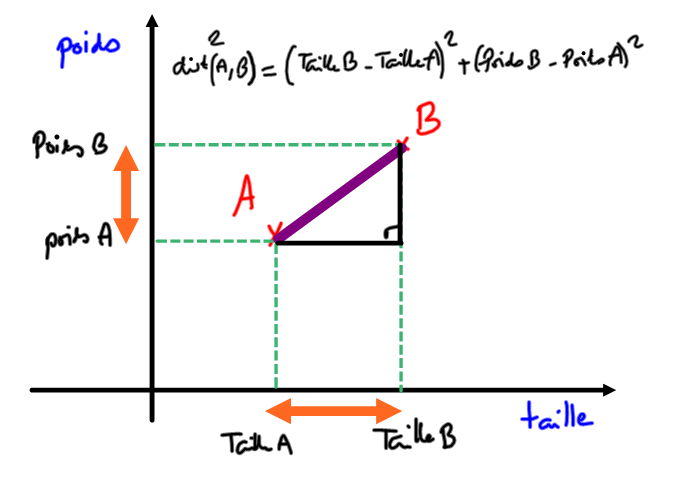
Le jeu de données : Top14

code lecture CSV

🐍 Script Python

import pandas as pd #import du module pandas, abrégé classiquement par "pd"

df = pd.read_csv('top14.csv', encoding = 'utf-8')

Résultat attendu :⚓︎

Il faut créer une fonction knn() qui prend en argument poids et taille , qui sont les caractéristiques du nouveau joueur. La fonction doit renvoyer une chaîne de caractère correspondant au poste auquel elle est susceptible de jouer.

Exemple :

code fonction KNN

🐍 Script Python

  def knn(poids, taille):
      #On ajoute une nouvelle colonne distance à notre jeu de données pandas
      #correspondant la la distance euclienne entre le nouveau et la ligne traitée
      df['distance']=(df['Taille']-taille)**2+(df['Poids']-poids)**2
      # On trie le jeu de donnée sur cette nouvelle colonne
      newdf = df.sort_values(by='distance', ascending=True)
      #On ne garde que les 6 premières lignes que l'on 'copie' dans un nouveau dataframe
      newdftri = newdf.head(6) #on prend les 6 joueurs les plus proches physiquement
      #On ne garde que le poste le plus fréquent sur ces 6 lignes
      sol = newdftri['Poste'].describe().top
      return sol
  knn(93,188)

Application⚓︎

Question 4

questionRéponse

Et si Nicola karabatic jouait au rugby, à quel poste jouerait-il ?

3ème ligne

Influence du paramètre \(k\)⚓︎

Dans le code précédent, on a travaillé avec \(k=6\) et c'est le poste majoritaire parmi les 6 joueurs les plus proches qui a été donné par l'algorithme.
Modifions légèrement la fonction knn() afin d'observer l'influence du paramètre \(k\) sur la prédiction :

🐍 Script Python

def knn(poids, taille, k):
  df['distance']=(df['Taille']-taille)**2+(df['Poids']-poids)**2
  newdf = df.sort_values(by='distance', ascending=True)
  newdftri = newdf.head(k) #on prend les k joueurs les plus proches physiquement
  sol = newdftri['Poste'].describe().top
  return sol

#On boucle pour déterminer pour k allant de 1 à 20 pour observer le résultat obtenu
for k in range(1,20):
    print(knn(93,188,k))

📋 Texte

Centre
Centre
Centre
Centre
Ailier
Centre
Ailier
Ailier
Ailier
Ailier
Ailier
Centre
Centre
Centre
Ailier
Ailier
Ailier
Ailier
Ailier

On s'aperçoit que la prédiction est très stable... sauf si \(k=1\) !
Il se trouve qu'un joueur possède exactement ces caractéristiques physiques (Pierre-Louis BARASSI) et qu'il joue Centre :

🐍 Script Python

df['distance']=(df['Taille']-188)**2+(df['Poids']-93)**2
newdf = df.sort_values(by='distance', ascending=True)
newdf.head(10)

On peut s'apercevoir aussi que jusqu'à \(k=5\), aucun poste n'est majoritaire : la prédiction pourrait aussi bien renvoyer Centre, 3ème ligne, ou Arrière. Ce n'est que grâce à l'ordre alphabétique que la réponse renvoyée est «Ailier». Par contre, dès que \(k \geqslant 5\), le poste d'Ailier est bien majoritaire parmi les \(k\) plus proches voisins.

Conclusion⚓︎

Que pouvez vous conclure sur l'influence du paramètre k ?
k n'est pas un paramètre mais un hyperparamètre, c'est-à-dire que contrairement aux paramètres classiques, il ne va pas pouvoir être appris automatiquement par l'algorithme à partir des données d'entraînement. Les hyperparamètres permettent de caractériser le modèle (complexité, rapidité de convergence, etc). Ce ne sont pas les données d'apprentissage qui vont permettre de trouver ces paramètres (en l'occurrence ici, le nombre de voisins k), mais bien à nous de l'optimiser à l'aide du jeu de données test.